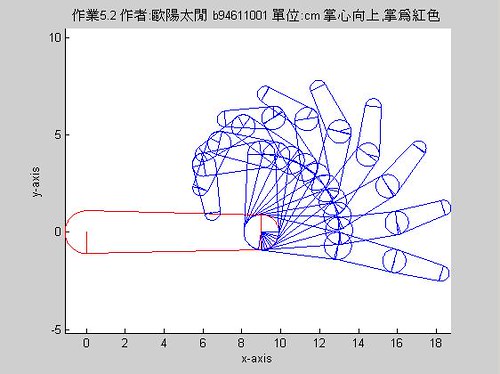
本週四 (4/26)曾來上課。
根據題目:
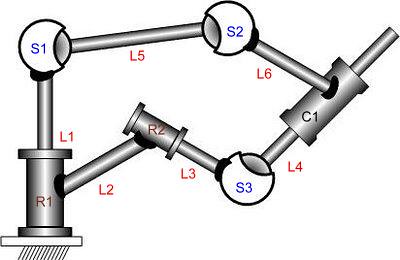
四連桿,其桿長分別為r=[4 3 3 5],由桿2驅動,設第一固定桿角度theta1=0度; 角速度 td2=10rad/s; 角加速度tdd2=0 rad/s^2。
一 ,設桿2角度theta2=45度時,運動學分析
採用老師機動學教學部落格中提供的f4bar程式(f4bar程式之輸出之第七行夾角並未輸出)註解後版本如附件一
其中:
r(1:4) = [4 3 3 5] %各桿之長度
theta1 = 0 deg %第一桿水平角
theta2 = 45 deg %驅動桿水平夾角
td2 = 10 %驅動桿(第二桿)角速度
tdd2 = 0 %驅動桿(第二桿)角加速度
mode = -1 %閉合型
linkdrive = 0 %驅動桿第二桿
>> r(1:4) = [4 3 3 5]
t1=0
t2=45
ang=10
aacc=0
f4bar(r,t1,t2,ang,aacc,-1,0)
ans =
1.0e+003 *
0.0040 0 0 0
0.0021 + 0.0021i 0.0450 0.0100 0
0.0011 + 0.0028i 0.0695 -0.0163 0.4914
-0.0008 + 0.0049i 0.0995 -0.0050 0.3836
0.0212 + 0.0212i 0.0021 + 0.0021i
0.0041 - 0.0245i 0.0032 + 0.0049i
-0.2121 - 0.2121i 0
-1.8712 - 0.4391i 0
可得以下分析:
即各桿之(*1000)
位置 角度(度數) 角速度 角加速度
桿1 0.0040 0 0 0
桿2 0.0021 + 0.0021i 0.0450 0.0100 0
桿3 0.0011 + 0.0028i 0.0695 -0.0163 0.4914
桿4 -0.0008 + 0.0049i 0.0995 -0.0050 0.3836
Q速度 0.0212 + 0.0212i Q位置 0.0021 + 0.0021i
P速度 0.0041 - 0.0245i P位置 0.0032 + 0.0049i
Q加速 -0.2121 - 0.2121i
P加速 -1.8712 - 0.4391i
f4bar之程式似乎與網頁之說明有所不同,程式中註解data (1,6),data (2,6)分別為Q,P位置,但網頁為VQ,AQ,VP,AP之絕對值
二,四連桿位置及各點速度
由於需繪出一四連桿系統並撰寫一程式繪製之,故參考機動學教學平台主題6.1至6.5關於四連桿系統的位置,速度,加速度之分析,並據此撰寫一
函式以利日後使用.
由於教學平台之範例程式為以直線來表現連桿,故試寫一函式嘗試以連桿圖形來顯示實際的運動狀況,基礎架構仍同於drawlinks.m,概述如下:
1.輸入防呆處理
2.提取f4bar分析的結果
3.進行計算,產生繪圖用數據
4.進行繪圖
5.數據標示及顯示(P,Q桿端速度)
執行結果如下:
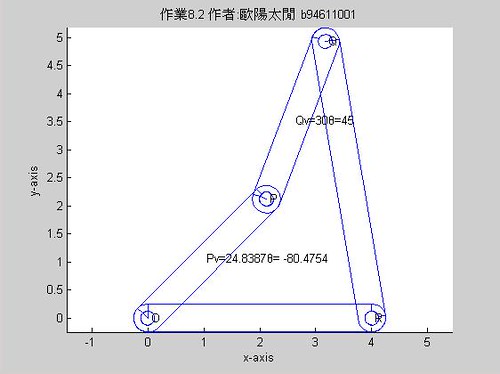
script如下:
title('作業8.2 作者:歐陽太閒 b94611001');%資訊
xlabel('x-axis');
ylabel('y-axis');
dw4shape([4 3 3 5],0,45,10,0,-1,0);
dw4shape程式碼如下:
function [values]=dw4shape(r,th1,th2,td,tdd,mode,linkdrive)
%歐陽太閒 b94611001
%本函數改寫自老師的drawlinks.m
%[values]=dw4shape(四桿長,第一桿角度,第二桿角度,角速度,角加速度,模式,驅動桿)
%[values]=dw4shape([4 3 3 5],0,45,10,0,-1,0)
%本程式需要f4bar.m及linkshape.m方能正常執行
r2d=180/pi;
axis equal;
if nargin<7,linkdrive=0;end %防呆
if nargin<6,mode=1;end %防呆
[values b]=f4bar(r,th1,th2,td,tdd,mode,linkdrive); %提取f4bar中的值
rr=values(:,1);
rr(3,1)=rr(1,1)+rr(4,1);
rx=real(rr(:,1));rx(4)=0;
ry=imag(rr(:,1));ry(4)=0;
qv=abs(values(1,5)); %取得點Q速度
if real(real(values(1,5)))>0;dirqv=atan(imag(values(1,5))/real(values(1,5)))*r2d;else;dirqv=pi/2;end %方向
pv=abs(values(2,5)); %取得點P速度
if real(real(values(2,5)))>0;dirpv=atan(imag(values(2,5))/real(values(2,5)))*r2d;else;dirpv=pi/2;end %方向
if b==1
linkshape([0 0],[rx(1),ry(1)],0.5); %第一桿
hold on;
if linkdrive==0 %第二桿為驅動桿時
linkshape([0 0],[rx(2),ry(2)],0.5); %繪製第二桿
linkshape([rx(2) ry(2)],[rx(3),ry(3)],0.5); %繪製第三桿
else
linkshape([0 0],[rx(2),ry(2)],1); %繪製第二桿
linkshape([rx(2) ry(2)],[rx(3),ry(3)],0.5);%繪製第三桿
end
linkshape([rx(3) ry(3)],[rx(1),ry(1)],0.5);%繪製第四桿
end
text(0,0,' O');
text(rx(1),ry(1),' R');
text(rx(2),ry(2),' P');
text(rx(2)/2,ry(2)/2, ['Pv=' num2str(pv) 'θ= ' num2str(dirpv)]);%標示P速度
text(rx(3),ry(3),' Q');
text((rx(3)-rx(2))/2+rx(2),(ry(3)-ry(2))/2+ry(2),['Qv=' num2str(qv) 'θ=' num2str(dirqv)]);%標示Q速度
%程式結束
另外,若以圖形方式呈現(由於圖形速度加速度過大,故未完整顯示),可在dw4shape末端加入以下程式碼
藍色為Q點速度,紅色為P點速度,黃色為Q點加速,粉紅色為P點加速
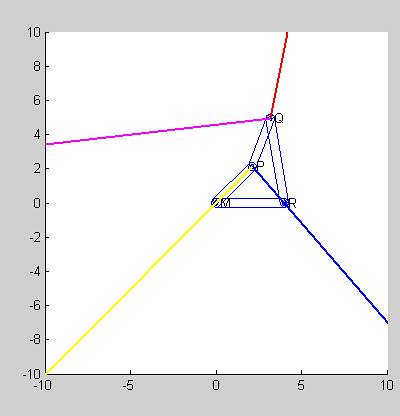
可利用以下程式碼:
qvx=real(values(1,5))
qvy=imag(values(1,5))
line([rx(2) rx(2)+qvx],[ry(2) ry(2)+qvy],'color','b','linewidth',2) %藍色為Q點速度
pvx=real(values(2,5))
pvy=imag(values(2,5))
line([rx(3) rx(3)+pvx],[ry(3) ry(3)+pvy],'color','r','linewidth',2) %紅色為P點速度
qax=real(values(3,5))
qay=imag(values(3,5))
line([rx(2) rx(2)+qax],[ry(2) ry(2)+qay],'color','y','linewidth',2) %黃色為Q點加速
pax=real(values(4,5))
pay=imag(values(4,5))
line([rx(3) rx(3)+pax],[ry(3) ry(3)+pay],'color','m','linewidth',2) 粉紅色為P點加速
axis equal;grid on
axis([-30 30 -30 30]);
若採用老師的drawlinks
title('作業8.2 作者:歐陽太閒 b94611001');%資訊
xlabel('x-axis');
ylabel('y-axis');
drawlinks([4 3 3 5],0,45,-1,0);
則其結果為
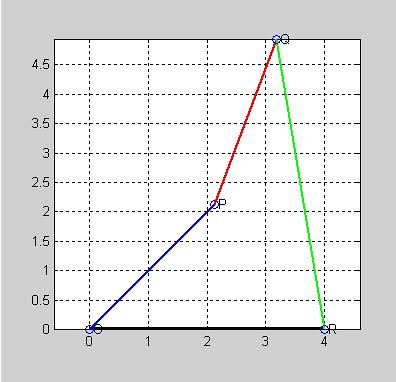
三,四連桿之限制角度
由於四連桿運動機構中有死點存在,故需撰寫一程式進行分析找尋驅動桿可運動的範圍
而本程式中利用機動學教學部落格中的fb_angle_limits.m進行角度分析
其結構如下:
1.程式資訊
2.自fb_angle_limits取得角度分析的資訊
3.以此資訊進行繪製
4.數據標示
script如下:
>>dw4lim([4 3 3 5],0,-1,0)
angs =
28.9550 (最小角)
ange =
331.0450 (最大角)
執行結果:
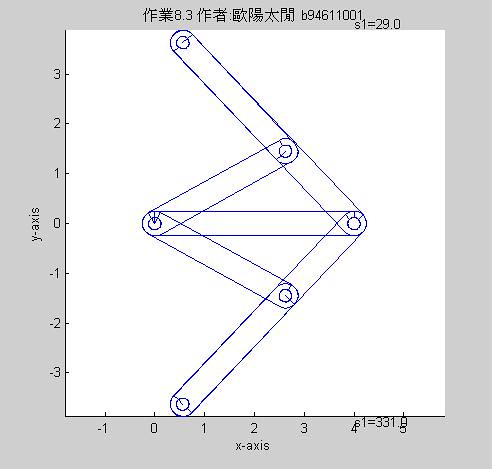
function dw4lim(r,th1,sigma,driver)
%歐陽太閒 b94611001
%dw4lim(四桿長,第一桿角度,模式,驅動桿)
%本程式用於進行尋找四連桿系統的驅動桿最大角及最小角
%本程式需有 dw4shape.m 及 fb_angle_limits.m方可正確執行
title('作業8.3 作者:歐陽太閒 b94611001');%資訊
xlabel('x-axis');
ylabel('y-axis');
[angs, ange]=fb_angle_limits(r,th1,driver) %利用fb_angle_limits進行分析
dw4shape(r,th1,Qstart,0,0,sigma,driver); %程式碼再利用
dw4shape(r,th1,Qstop,0,0,sigma,driver);
text(r(1),r(1),['s1=' num2str(angs,'%6.1f')]); %取到小數下第一位並轉成字串
text(r(1),-r(1),['s1=' num2str(ange,'%6.1f')]);
%程式結束
而若以老師的drawlimits進行分析:
drawlimits([4 3 3 5],0,-1,0)
Qstart =
28.9550 (最小角)
Qstop =
331.0450 (最大角)
執行結果:
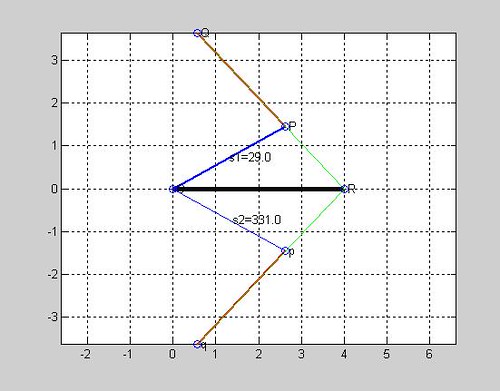
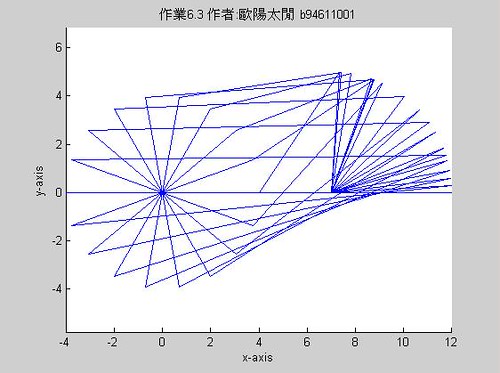
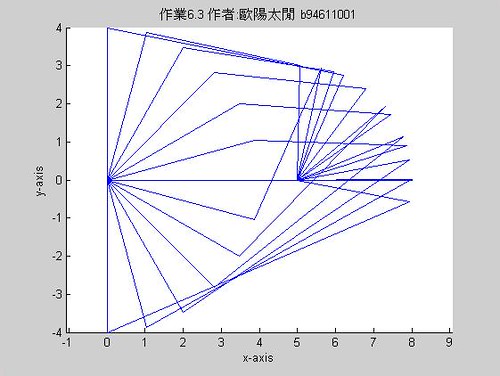
四,設theta2=[0:20:360],試繪出此組四連桿之重疊影像,解釋為何有些沒有值。
本程式繪出四連桿的連續運動並顯示其驅動桿之旋轉有一範圍,亦即沒有值處乃是來自於其在f4bar的分析結果中乃是不存在的(虛數)
是故,即如老師在課堂上所說的,其沒有值處是由於其解為虛數,在實數座標系中不能顯現.
script如下:
title('作業8.4 作者:歐陽太閒 b94611001');%資訊
xlabel('x-axis');
ylabel('y-axis');
for k=[0:20]
dw4shape([4 3 3 5],0,k*20,10,0,-1,0);
end
執行結果:
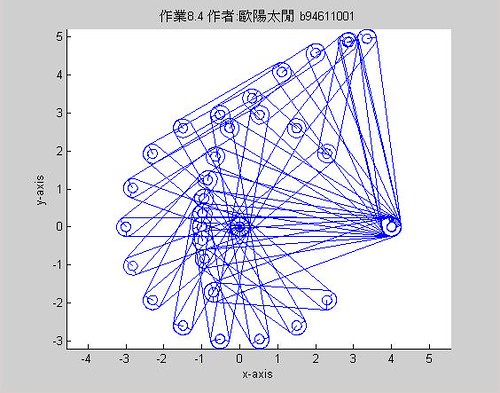
而若以drawlinks為之
script如下:
title('作業8.4 作者:歐陽太閒 b94611001');%資訊
xlabel('x-axis');
ylabel('y-axis');
for k=[0:20]
drawlinks([4 3 3 5],0,k*20,-1,0);
end
結果:
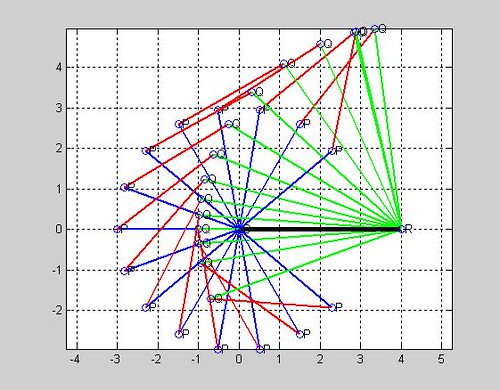
Combination of links fail at degrees 0.0
Combination of links fail at degrees 20.0
Combination of links fail at degrees 340.0
Combination of links fail at degrees 360.0
Combination of links fail at degrees 380.0
即為fbar中傳回b不為1,不能組合的無效結果,也就是在驅動桿運動範圍外的結果.
五,動畫
根據老師的drawlimit執行結果:
drawlimits([4 3 3 5],0,-1,0)
Qstart =
28.9550
Qstop =
331.0450
故可知其可旋轉範圍為28.9550 2到331.0450之間
可寫一程式使其迴轉:
其結構如下
1.資訊
2.for-loop進行繪製
程式碼如下:
title('作業8.5 作者:歐陽太閒 b94611001');%資訊
xlabel('x-axis');
ylabel('y-axis');
r=[4 3 3 5]
for k=[29:331] %簡化程式碼
pause(0.01);
clf;
axis([-8 8 -5 5]); %固定座標系
dw4shape(r,0,k,0,0,-1,0) %採用先前撰寫的dw4shape
end
結果如下:
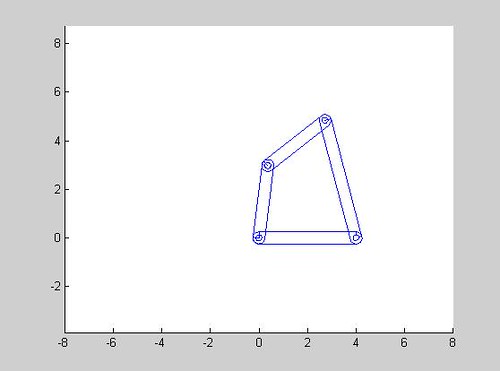
影片連結
經老師指導,本影片已經改進為坐標不移動
心得:
本次作業雖可參考教學平台之資料,但仍在實際處理上遇到很多困難,其大多來自於角度分析時定義的限制,所以必須要使用複雜的if-then-else
結構來進行處理,而四連桿系統的運動本就複雜難以分析,故前人累積的智慧,使我們不必重新從頭想起,而可以以現成的公式,定理等進行處理.
而本次作業也已經進入到分析實際運用於生活中的結構,表面上看來簡單,實際上卻極為複雜.
附件一
%歐陽太閒 b94611001 加註
function [data,form] = f4bar(r,theta1,theta2,td2,tdd2,mode,linkdrive)
%
%function [data,form] = f4bar(r,theta1,theta2,td2,tdd2,mode,linkdrive)
% This function analyzes a four-bar linkage when the driving link is
% crank or coupler. The input data are:
% theta1,theta2 are angles in degrees
% r=[r1 r2 r3 r4]= lengths of links(1=frame)
%td2 = crank or coupler angular velocity (rad/sec)
%tdd2 = crank or coupler angular acceleration (rad/sec^2)
%mode = +1 or -1. Identifies assembly mode
%linkdrive = 0 for crank as driver; 1 for coupler as driver
%data (1:4,1) = link positions for 4 links
%data (1:4,2) = link angles in degrees
%data (1:4,3) = link angular velocities
%data (1:4,4) = link angular accelerations
%data (1,5) = velocity of point Q
%data (2,5) = velocity of point P
%data (3,5) = acceleration of point Q
%data (4,5) = acceleration of point P
%data (1,6) = position of Q %和網頁說明不同
%data (2,6) = position of P
%form = assembly status. form = 0, mechanism fails to
% assemble.
% program revised from Waldron's Textbook
% Revised:DSFON, BIME, NTU. Date: Feb. 7, 2007
if nargin<7,linkdrive=0;end %防呆裝置 補足驅動
if nargin<6,mode=1;end %防呆裝置 補足模數
data=zeros(4,6); %建立4*6的零矩陣
% if coupler is the driver, interchange the vetor 3 & 2
if linkdrive==1,r=[r(1) r(3) r(2) r(4)];end %驅動桿為第三桿時,r的順序交換
rr=r.*r;d2g=pi/180;
[theta,td,tdd]=deal(zeros(4,1)); %存到theta,td,tdd
theta(1:2)=[theta1 theta2]*d2g; %theta1,theta2的輸入為角度量非徑度量
t1=theta(1);tx=theta(2);
s1=sin(t1);c1=cos(t1); %分別取t1,tx的水平和垂直分量
sx=sin(tx);cx=cos(tx);
% position calculations %取位置
A=2*r(1)*r(4)*c1-2*r(2)*r(4)*cx;
C=rr(1)+rr(2)+rr(4)-rr(3)-2*r(1)*r(2)*(c1*cx+s1*sx);
B=2*r(1)*r(4)*s1-2*r(2)*r(4)*sx;
pos=B*B-C*C+A*A;
if pos>=0, %pos>0時可組合
form=1;
% Check for the denominator equal to zero
if abs(C-A)>=1e-5 %避免分母為零,採用一小數字為分界
t4=2*atan((-B+mode*sqrt(pos))/(C-A));
s4=sin(t4);c4=cos(t4);
t3=atan2((r(1)*s1+r(4)*s4-r(2)*sx),(r(1)*c1+r(4)*c4-r(2)*cx));
s3=sin(t3);c3=cos(t3);
else
% If the denominator is zero, compute theta(3) first 分母為零先計算theta(3)
A=-2*r(1)*r(3)*c1+2*r(2)*r(3)*cx;
B=-2*r(1)*r(3)*s1+2*r(2)*r(3)*sx;
C=rr(1)+rr(2)+rr(3)-rr(4)-2*r(1)*r(2)*(c1*cx+s1*sx);
pos=B*B-C*C+A*A;
if pos>=0,
t3=2*atan((-B-mode*sqrt(pos))/(C-A));
s3=sin(t3); c3=cos(t3);
t4=atan2((-r(1)*s1+r(3)*s3+r(2)*sx),...
(-r(1)*c1+r(3)*c3+r(2)*cx));
s4=sin(t4);c4=cos(t4);
end
end %theta(3),theta(4)計算完畢
theta(3)=t3;theta(4)=t4;
%velocity calculation %速度分析計算
td(2)=td2;
AM=[-r(3)*s3, r(4)*s4; -r(3)*c3, r(4)*c4]; %r3,r4分別乘上其對應角度的sin,cos化為分量
BM=[r(2)*td(2)*sx;r(2)*td(2)*cx]; %乘上角速度和方向分量
CM=AM\BM; %求解([RM] [AM] = [CM]公式,6.2)
td(3)=CM(1);td(4)=CM(2); %得速度
%acceleration calculation %加速度分析計算
tdd(2)=tdd2; %類似速度分析計算的作法
BM=[r(2)*tdd(2)*sx+r(2)*td(2)*td(2)*cx+r(3)*td(3)*td(3)*c3-...
r(4)*td(4)*td(4)*c4;r(2)*tdd(2)*cx-r(2)*td(2)*td(2)*sx-...
r(3)*td(3)*td(3)*s3+r(4)*td(4)*td(4)*s4];
CM=AM\BM; %求解([DM]=[RM]\[FM])
tdd(3)=CM(1);tdd(4)=CM(2); %得解
%store results in array data %將解格式化,存入矩陣以利處理
% coordinates of P and Q
if linkdrive==1,
c2=c3;c3=cx;s2=s3;s3=sx;
r(2:3)=[r(3) r(2)];theta(2:3)=[theta(3) theta(2)];
td(2:3)=[td(3) td(2)];tdd(2:3)=[tdd(3) tdd(2)];
else
c2=cx;s2=sx;
end
for j=1:4,
data(j,1:4)=[r(j)*exp(i*theta(j)) theta(j)/d2g td(j) tdd(j)] ;
end % position vectors
data(1,5)=r(2)*td(2)*exp(i*theta(2));%velocity for point Q %存入一開始建立的零矩陣
data(2,5)=r(4)*td(4)*exp(i*theta(4));%velocity for point P
data(3,5)=r(2)*(i*tdd(2)-td(2)*td(2))*exp(i*theta(2));%acc of Q
data(4,5)=r(4)*(i*tdd(4)-td(4)*td(4))*exp(i*theta(4));%acc of P
data(1,6)=data(2,1);%position of Q, again
data(2,6)=data(1,1)+data(4,1);% position of P
%find the accelerations
else
form=0; %處理form=0時
if linkdrive==1,
r=[r(1) r(3) r(2) r(4)];
for j=1:4, data(j,1)=r(j).*exp(i*theta(j));end % positions
end
end
%第八次作業結束
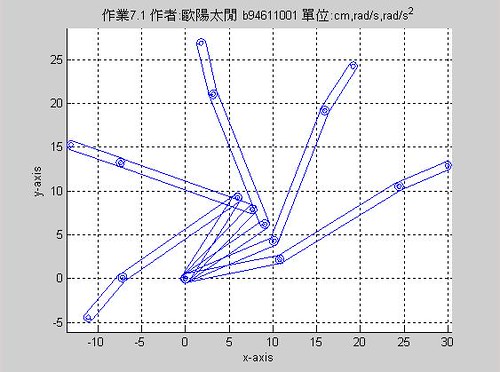 結果如圖
結果如圖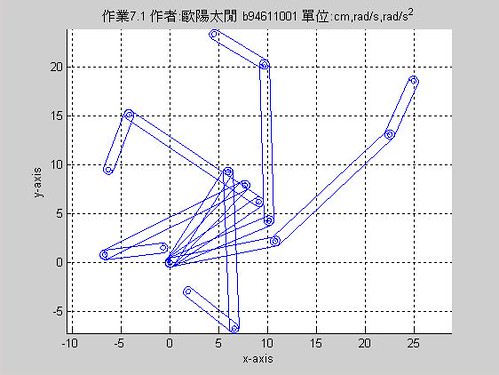 結果如圖
結果如圖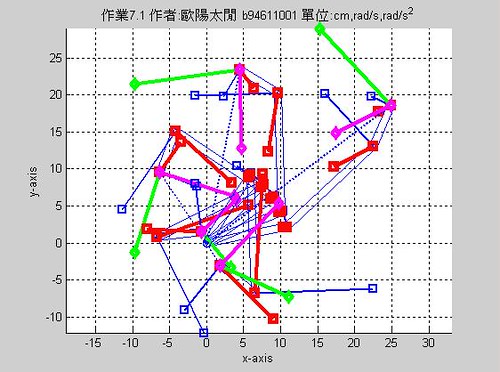 結果如圖
結果如圖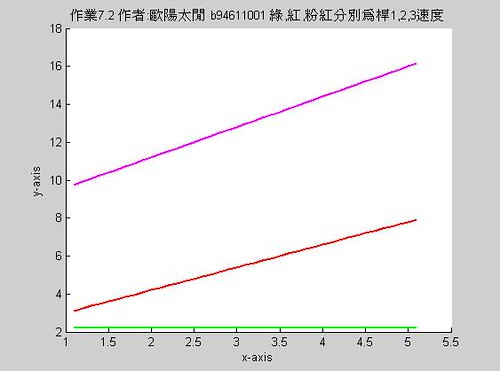 結果如圖
結果如圖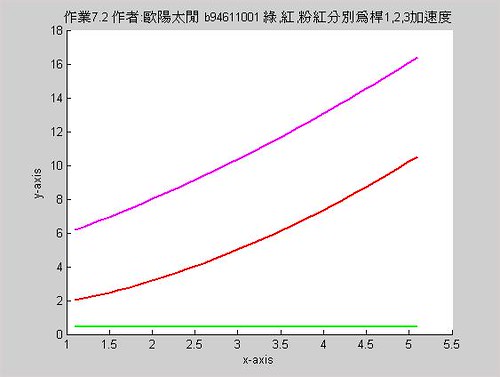 結果如圖
結果如圖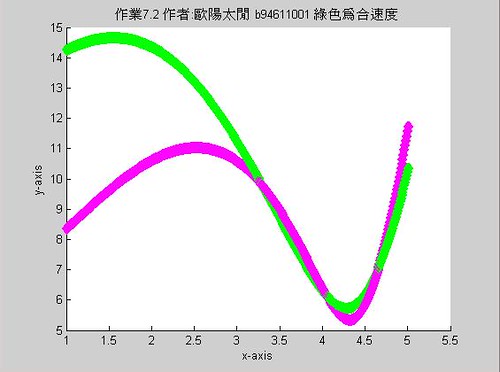 結果如圖
結果如圖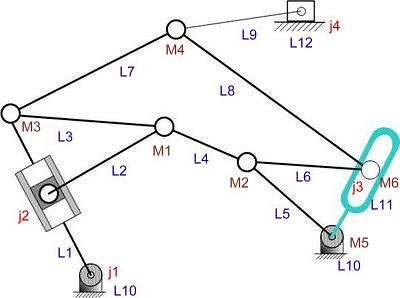


 結果如圖
結果如圖