本週(5/3)有來上課,組別A
於題目中可得:
曲桿長Rcm , 連桿Lcm,滑塊之偏置量為10cm,R=10+1=11,L=R+5=16
無初始速度或加速度,
故可得以下參數:(單位cm)
r(1) =固定桿 =會自行改變設0
r(2) =曲桿 =11
r(3) =結合(連)桿=16
r(4) =垂直偏置量=10
theta1 =第一桿之水平角=0
theta2 = 驅動桿之水平夾角=於計算時代入
td2 = 驅動桿角速度=0
tdd2 = 驅動桿角加速度=0
sigma = 1 組合模數,其中組合模數之閉合或分枝會導致左右鏡像的結果.
driver = 0 驅動桿為第二桿
1 驅動桿為第三桿
2 滑塊驅動
權衡各種分析方法後,使用單純的三角函數處理(如課本)由於反三角函數定義的關系,可能會面臨需撰寫大量if判斷式,且除錯不易的窘境,而Euler化可以大幅簡化計算,就如同電工學的交流電多相合成,複數計算遠較和差化積有效率的多.
故以下作業都將利用老師的sldlink.m(複數計算),sld_angle_limits.m,進行分析
形式:
sldlink(r,theta1,theta2,td2,tdd2,sigma,driver)注解參考附件一
sld_angle_limits(r,theta1,linkdrive) 注解及修改參考附件二
drawsldlimits(r,th1,sigma,driver)
drawsldpaths(r6,th6,r,th1,theta,td2,tdd2,sigma,npts,driver,mode) 注解及修改參考附件三
其中sldlink有部分程式碼在matlab 6.5中運作有問題,即
%f=@(num,ndg);
%round(num*10^ndg)/10^ndg; %取整數
%arg=f(arg,5);
等,但加注解化後對運作無太大影響
一,運動的界限範圍
首先利用老師撰寫的sld_angle_limits代入以下參數進行分析:
1.桿2為驅動桿
r=[0 11 16 10];
theta1=0;
linkdrive=0;
sld_angle_limits(r,theta1,linkdrive);
得到:
Qstart =
3.6000e-006
Qstop =
360.0000
顯然不符,檢查sld_angle_limits程式碼後發現其中缺少了r3≧r4≧0,r3+r4≧r2(即講義7.4.2)之情況
故在其中加入以下程式碼
elseif r3+r4>=r2 & r3>=0 & r3>=r4
Qstart=asin((r4-r3)/r2)
Qstop=pi- asin((r4-r3)/r2)
才能得到:
θmin =θ1 + sin-1((r4-r3) / r2) =asin((10-16)/11)= -0.5769=-33
θmax =θ1 +π- sin-1((r4-r3) / r2) =pi-asin((10-16)/11)=3.7185=213
即
drawsldlimits([0 11 16 10],0,1,0)
Qstart = (起始角)
-33.0557
Qstop = (結束角)
213.0557
其中OP為桿2,PQ為桿3,QR為偏置量
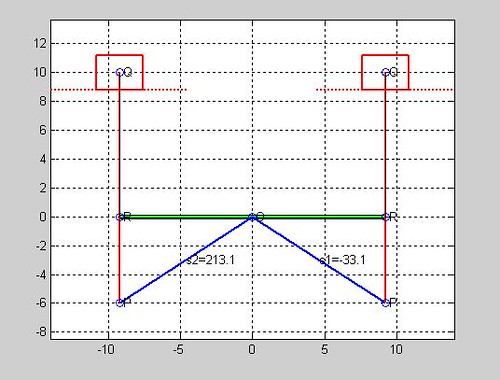 結果如圖
結果如圖亦可產生
動畫
for k=[-33:213] %簡化程式碼
pause(0.01);
clf;
dwsldshape([0 11 16 10],0,k,1,0)
axis([-16 30 -16 16]); %固定座標系
end
因此:
2.桿3為驅動桿時:
drawsldlimits([0 11 16 10],0,-1,1)
Qstart =
-3.5833
Qstop =
183.5833
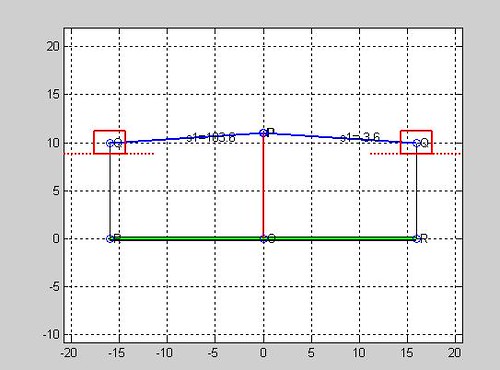 結果如圖
結果如圖3.滑塊為驅動桿時:
drawsldlimits([0 11 16 10],0,-1,2)
Qstart =
-25.0799
Qstop =
25.0799
 結果如圖
結果如圖二,位置分析
由於各點以連桿連結,故參考老師的drawsldlinks.m撰寫如下程式:
其架構如下:
1.資訊
2.將參數放入sldlink且傳回結果
3.複數化
4.若組合存在則繪制
1.接地桿
2.依參數繪桿
3.表示偏心量
4.繪滑塊
5.不能組合時訊息
function [values]=dwsldshape(r,th1,th2,sigma,driver)
%參考老師的drawsldlinks.m
%歐陽太閒 b94611001
%需用到linkshape.m,sldlink.m,sldbox.m
title('作業9.2 作者:歐陽太閒 b94611001');%資訊
xlabel('x-axis');
ylabel('y-axis');
axis equal
grid on
[values b]=sldlink(r,th1,th2,10,0,sigma,driver); %將參數放入sldlink且傳回分析結果
rr=values(:,1);
rr(3)=rr(3)+rr(2);
rx=real(rr);rx(4)=0;%複數化
ry=imag(rr);ry(4)=0;
if b==1
linkshape([0 0],[rx(1) 0]); %繪接地桿
hold on;
linkshape([0 0],[rx(1) ry(1)]); %繪桿2,驅動桿問題已有sldlink處理
linkshape([0 0],[rx(2) ry(2)]); %繪桿3
linkshape([rx(2) ry(2)],[rx(3) ry(3)]);
plot([rx(1) rx(3)],[ry(1) ry(3)],'r-'); % 偏心量,滑塊為重力外力閉合
plot(rx,ry,'bo');
text(0,0,' O');text(rx(1),ry(1),' R');
text(rx(2),ry(2),' P');text(rx(3),ry(3),' Q');
length=max(abs(values(2:3,1))); %產生滑塊用參數
len=.20*length;ww=.15*length;
[coords] = sldbox(len,ww,rx(3),ry(3),th1); %畫出滑塊
plot(coords(:,1),coords(:,2),'r-','LineWidth',2);
[coords] = sldbox(len*3,0,rx(3),ry(3)-ww/2,th1);
plot(coords(:,1),coords(:,2),'r:','LineWidth',1.5);
else
fprintf('無法組成,角度%6.1f\n',th2); %不能組成時訊息
end
1.桿2為驅動桿(以角度60度為例)
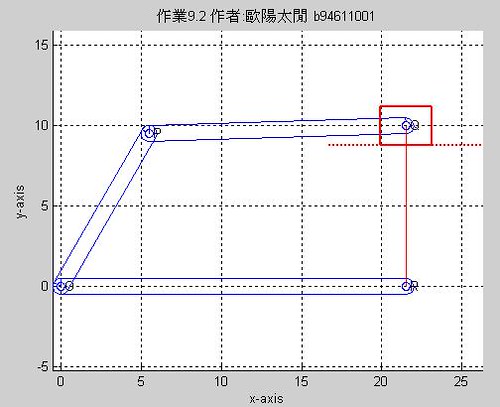 結果如圖
結果如圖可解析如下
ans =
1.0e+003 *
Columns 1 through 4
桿1位 0.0215 桿1角 0 桿1角速度 0 桿1角加速度 0
桿2位 0.0055 + 0.0095i 桿2角 0.0600 桿2角速度 0.0100 桿2角加速度 0
桿3位 0.0160 + 0.0005i 桿3角 0.0017 桿3角速度 -0.0034 桿3角加速度 0.0599
桿4位 0.0000 + 0.0100i 桿4角 0.0900 桿4角速度 0 桿4角加速度 0
Columns 5 through 8
軸向速度 -0.0936 q速度 -0.0953 + 0.0550i(abs) 0.1100 q速度角度0.1500
軸向加速 -0.7675 p速度 -0.0936 (abs) 0.0936 p速度角度0.1800
Q位置向量 0.0055 + 0.0095i q加速度-0.5500 - 0.9526i(abs) 1.1000 q加速度角度-0.1200
P位置向量 0.0215 + 0.0100i p加速度-0.7675 (abs) 0.7675 p加速度角度 0.1800
2.桿3為驅動桿(以角度60度為例)
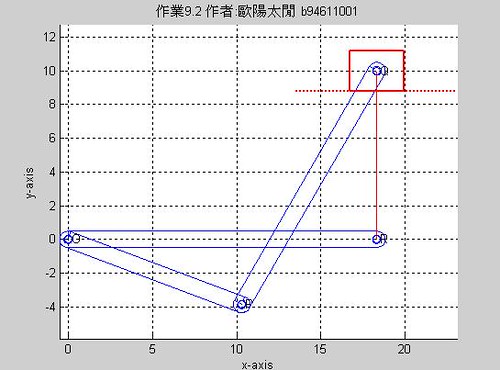 結果如圖
結果如圖dwsldshape([0 11 16 10],0,60,1,1)
ans = (解析同9-二-1)
1.0e+003 *
Columns 1 through 4
0.0183 0 0 0
0.0103 - 0.0039i -0.0205 -0.0078 0.1119
0.0080 + 0.0139i 0.0600 0.0100 0
0.0000 + 0.0100i 0.0900 0 0
Columns 5 through 8
-0.1685 -0.0299 - 0.0800i 0.0854 -0.1105
-0.9896 -0.1685 - 0.0000i 0.1685 -0.1800
0.0103 - 0.0039i -0.1896 + 1.3856i 1.3986 0.0978
0.0183 + 0.0100i -0.9896 0.9896 0.1800
3.滑塊為驅動桿(以角度60度為例)
dwsldshape([0 11 16 10],0,60,1,2)
 結果如圖
結果如圖ans = (解析同9-二-1)
1.0e+002 *
Columns 1 through 4
0 0 0 0
-0.1086 - 0.0175i -1.7085 -0.0100 -0.0108
0.1086 + 0.1175i 0.4725 -0.0100 -0.0016
0.0000 + 0.1000i 0.9000 0 0
Columns 5 through 8
0.1000 -0.0175 + 0.1086i 0.1100 0.9915
0 0.1000 0.1000 0
-0.1086 - 0.0175i 0.0897 + 0.1350i 0.1621 0.5641
0 + 0.1000i 0 0 0
三,路徑分析
而講義7.5提到,可用drawsldpaths.m整合sldlink,body,fb_sld_linits及drawlinks
其中最重要的,便是其可輸出非常漂亮的速度,加速度,角速度,角加速度隨角度變化圖表
以及系統的連續運動路徑
drawsldpaths(r6,th6,r,th1,theta,td2,tdd2,sigma,npts,driver,mode)
r= [0 11 16 10] 各桿長
th1=0 第一桿角度
th2=0 驅動桿或聯結桿角度
td2=0 驅動桿之角速度
tdd2=0 角加速度。
sigma=1 組合模數
driver= 0 曲桿驅動
1 連桿驅動
2 滑塊驅動
Npts=50 分割點數
r6,rh6,nlink:桿上特定點之位置,包括桿長,與桿之夾角及附於何桿。
mode=1 畫所有圖表
由於程式在Matlab6.5下繪制alphapatch會導致畫面混亂,故修改程式,
去除在本分析中用不到的延伸部分,即:
patch('xdata',real(para(1:3)),'ydata',imag(para(1:3)),...
'facecolor','r','facealpha',0.6,'marker','o');hold on;
plot(para(2),'bo');
(請見附件三)
故可得:
1.桿2為驅動桿
drawsldpaths(0,0,[0 11 16 10],0,0.01,0.01,1,50,0,1)
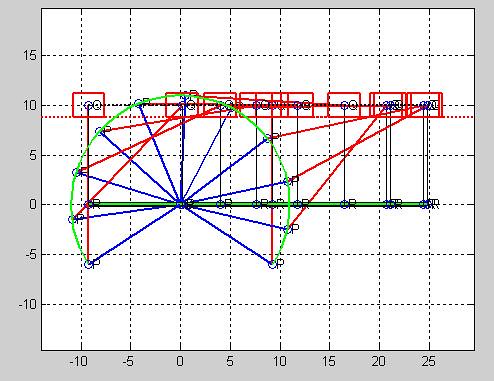 結果如圖
結果如圖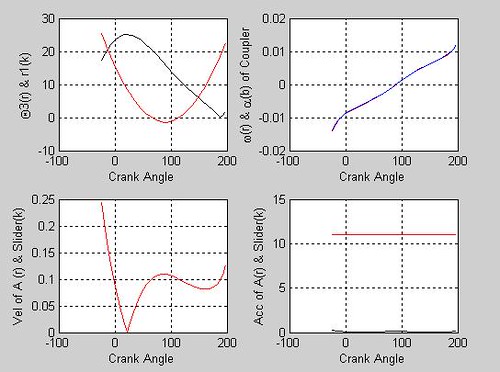 結果如表
結果如表2.桿3為驅動桿
drawsldpaths(0,0,[0 11 16 10],0,0.01,0.01,1,50,1,1)
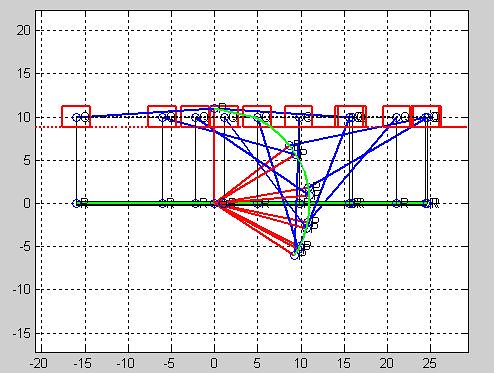 結果如圖
結果如圖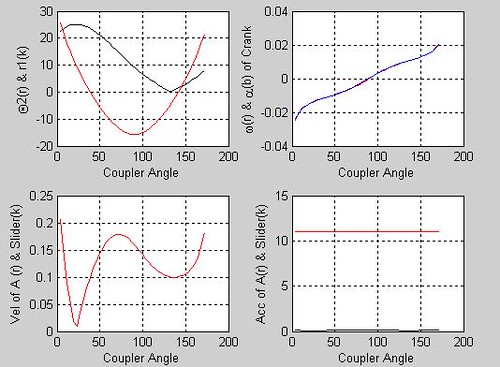 結果如表
結果如表3.滑塊為驅動桿
drawsldpaths(0,0,[0 11 16 10],0,0.01,0.01,2,50,2,1)
 結果如圖
結果如圖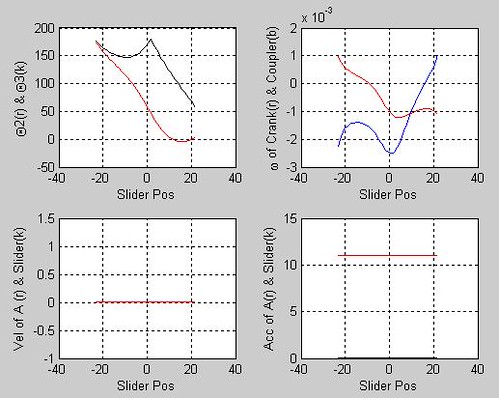 結果如表
結果如表心得:
本次作業為整體性的對一個系統進行分析,故所需用到的程式資源相當的大,且有許多部分需自行改寫,不過也操作的過程中體會MATLAB的強大.
附件一
function [data,form] = sldlink(r,theta1,theta2,td2,tdd2,sigma,driver)
%f=@(num,ndg) round(num*10^ndg)/10^ndg; %取整數,在6.5版會造成無法正確執行的問題
data=zeros(4,8); %生成一個4x8的零矩陣
if driver==1, r(2:3)=[r(3) r(2)];end %桿三為驅動桿時對換
rr=r.*r;d2g=pi/180; %數學運算部分
theta=[theta1 theta2 0 theta1+90]*d2g;
t1=theta(1);t4=theta(4);
[td,tdd,rd,rdd]=deal(zeros(4,1));
s1=sin(t1);c1=cos(t1); %轉成直角坐標系
s4=sin(t4);c4=cos(t4);
switch driver %驅動元件選擇
case 2 %滑塊驅動桿
rd(1)=td2; %傳入速度與加速度
rdd(1)=tdd2;
A=-2*r(1)*r(2)*c1-2*r(2)*r(4)*c4;
B=-2*r(1)*r(2)*s1-2*r(2)*r(4)*s4;
C=rr(1)+rr(2)+rr(4)-rr(3)+2*r(1)*r(4)*(c1*c4+s1*s4);
arg=B*B-C*C+A*A;
% arg=f(arg,5); %避免6.5出錯
if (arg>=0)
form=1; %assembly flag
t2=2*atan((-B+sigma*sqrt(arg))/(C-A));
s2=sin(t2); c2=cos(t2);
t3=atan2((r(1)*s1+r(4)*s4-r(2)*s2),(r(1)*c1+r(4)*c4-r(2)*c2));
theta(2)=t2; theta(3)=t3;
s3=sin(t3); c3=cos(t3);
%velocity calculation %速度計算
AM=[-r(2)*s2, -r(3)*s3; r(2)*c2, r(3)*c3];
BM=[rd(1)*c1;rd(1)*s1];
CM=AM\BM;
td(2)=CM(1); td(3)=CM(2);
%acceleration calculation %加速度計算
BM=[r(2)*td(2)*td(2)*c2+r(3)*td(3)*td(3)*c3+rdd(1)*c1;...
r(2)*td(2)*td(2)*s2+r(3)*td(3)*td(3)*s3+rdd(1)*s1];
CM=AM\BM;
tdd(2)=CM(1); tdd(3)=CM(2);
else
form=0; return; %無法連接時跳出
end
case {0,1} % for link 2 or 3 as a crank%桿2或桿3為曲桿
td(2)=td2; tdd(2)=tdd2; tx=theta(2);
sx=sin(tx); cx=cos(tx);
% position calculations %位置分析
A=2*r(4)*(c1*c4+s1*s4)-2*r(2)*(c1*cx+s1*sx);
B=rr(2)+rr(4)-rr(3)-2*r(2)*r(4)*(cx*c4+sx*s4);
arg=A*A-4*B;
%arg=f(arg,5); %避免6.5錯誤
if (arg>=0)
form=1; %assembly flag
r(1)=(-A+sigma*sqrt(arg))/2;
t3=atan2((r(1)*s1+r(4)*s4-r(2)*sx),(r(1)*c1+r(4)*c4-r(2)*cx));
theta(3)=t3;
s3=sin(t3); c3=cos(t3);
%velocity calculation %速度分析
AM=[c1, r(3)*s3; s1, -r(3)*c3];
BM=[-r(2)*td(2)*sx;r(2)*td(2)*cx];
CM=AM\BM;
rd(1)=CM(1); td(3)=CM(2);
%acceleration calculation %加速度分析
BM=[-r(2)*tdd(2)*sx-r(2)*td(2)*td(2)*cx-r(3)*td(3)*td(3)*c3;...
r(2)*tdd(2)*cx-r(2)*td(2)*td(2)*sx-r(3)*td(3)*td(3)*s3];
CM=AM\BM;
rdd(1)=CM(1); tdd(3)=CM(2);
else
form=0; %不能連接時
if driver==1, %處理曲桿為3
r(2:3)=[r(3) r(2)];
for j=1:4, data(j,1)=r(j).*exp(i*theta(j));end % position vectors
end
return;
end
if driver==1,
r(2:3)=[r(3) r(2)]; %桿2,3的資料交換
c2=c3;c3=cx;s2=s3;s3=sx;
td(2:3)=[td(3) td(2)];
tdd(2:3)=[tdd(3) tdd(2)];
theta(2:3)=[theta(3) theta(2)];
elseif driver==0
c2=cx;s2=sx;
end
end % end of switch %結束判斷
for j=1:4, %將所得資料格式化輸出
data(j,1)=r(j).*exp(i*theta(j));
data(j,2:4)=[theta(j)/d2g,td(j),tdd(j)];
end
data(:,5)=[rd(1);rdd(1);data(2,1);data(2,1)+data(3,1)];
data(1,6)=i*r(2)*td(2)*exp(i*theta(2));
data(2,6)=data(1,6)+i*r(3)*td(3)*exp(i*theta(3));
data(3,6)=r(2)*(i*tdd(2)-td(2)*td(2))*exp(i*theta(2));
data(4,6)=data(3,6)+r(3)*(i*tdd(3)-td(3)*td(3))*exp(i*theta(3));
%[Vq;Vp;Aq;Ap]
data(1:4,7)=abs(data(1:4,6));data(1:4,8)=angle(data(1:4,6))/d2g;
附件2
function [Qstart, Qstop]=sld_angle_limits(r,theta1,linkdrive)
r1=r(1);r2=r(2);r3=r(3);r4=r(4);
g2d=180/pi;
switch linkdrive
case 0 %crank %曲桿驅動時
if r3+r4
Qstart=asin((r4-r3)/r2);
Qstop=asin((r4+r3)/r2);
elseif r3+r4>=r2 & r4>=r3 %講義程式碼缺少的部分
Qstart=asin((r4-r3)/r2); %r3≧r4≧0,r3+r4≧r2(即講義7.4.2)
Qstop=pi-asin((r4-r3)/r2);%
elseif r3-r4<=r2 & r4<0 & r3>=-r4
Qstart=asin((r4-r3)/r2);
Qstop=asin((r4+r3)/r2);
elseif r3-r4>=r2 & r3>=0 & -r4>=r3
Qstart=-pi-asin((r4+r3)/r2);
Qstop=asin((r4+r3)/r2);
elseif r3+r4>=r2 & r3>=0 & r3>=r4
Qstart=asin((r4-r3)/r2);
Qstop=pi- asin((r4-r3)/r2);
else
Qstart=0;Qstop=2*pi;
end
case 1 %coupler %連桿驅動時
if r2-r4<=r3 & r4>=0 & r2>=r4%分別為講義7.4 RRRP的各種限制
Qstart=asin((r4-r2)/r3)
Qstop=pi-asin((r4-r2)/r3)
elseif r2+r4
Qstart=asin((r4-r2)/r3)
Qstop=asin((r4+r2)/r3)
elseif r2+r4<=r3 & r4<=0 & r2+r4>=0
Qstart=-pi-asin((r4+r2)/r3)
Qstop=asin((r4+r2)/r3)
elseif r2-r4
Qstop=asin((r4+r2)/r3)
else %r2>=(r3+abs(r4))
Qstart=0;Qstop=2*pi;
end
case 2 %slider displacement %滑塊驅動
Qstart=0;Qstop=0;
arg2=(r2+r3)^2-r4^2
if abs(r2-r3)>=r4
arg1=(r2-r3)^2-r4^2
if arg1>0,Qstart=sqrt(arg1);end;
Qstop=sqrt(arg2)
else
if arg2<0, return; end
Qstart=sqrt(arg2);Qstop=-sqrt(arg2)
end
theta1=0;g2d=1
end %case %各種情況分析結束
if Qstop
Qstart=theta1+(Qstart+adjust)*g2d %輸出
Qstop=theta1+(Qstop-adjust)*g2d
附件3
function drawsldpaths(r6,th6,r,th1,td2,tdd2,sigma,npts,driver,mode)
clf;
figure(1);
warning off;
r(abs(r)
npoint=abs(npts); %分割點數
th2=linspace(Qstart,Qstop,npoint); %產生點向量
val=zeros(11,npoint);
for i=1:npoint,
if driver==2, r(1)=th2(i);end
[vr b]=sldlink(r,th1,th2(i),td2,tdd2,sigma,driver); %利用sldlink分析
[para]=body(r6,th6,vr,3); %yongbody畫延伸物(本分析沒有用到)
if mod(i,5)==0|i==1|i==npoint,
drawsldlinks(r,th1,th2(i),sigma,driver); %繪桿及塊
end
val(1:3,i)=[vr(1,1)+vr(4,1);vr(2,1);para(2)];%Sq,Sp,Sa %找q,p,a
switch driver
case 0 %桿2驅動
val(4:7,i)=[abs(vr(1,1));vr(3,2);vr(3,3);vr(3,4)];
case 1 %桿3驅動
val(4:7,i)=[abs(vr(1,1));vr(2,2);vr(2,3);vr(2,4)];
case 2 %滑塊驅動
val(4:7,i)=[abs(vr(2,2));vr(3,2);vr(2,3);vr(3,3)];
end
val(8:11,i)=[vr(1,5);para(4);vr(4,6);para(5);]; %存入矩陣
%Vs, Va, As, Aa
end
warning on; %路徑繪制
plot(val(1,:),'k-','LineWidth',1.5,'linestyle',':');% path of Q
plot(val(2,:),'k-','LineWidth',1.5);% path of P
plot(val(3,:),'g-','LineWidth',1.5);% path of A
axis equal
if mode==0, return;end;
% %數據分析
th2=th2(3:end-3);val=val(:,3:end-3);
title0={'Crank Angle','Coupler Angle','Slider Pos'};
title1={'\Theta3(r) & r1(k)', '\Theta2(r) & r1(k)',...
'\Theta2(r) & \Theta3(k)' };
title2={'Vel of A (r) & Slider(k)',...
'Acc of A(r) & Slider(k)' };
title3={'\omega(r) & \alpha(b) of Coupler',...
'\omega(r) & \alpha(b) of Crank',...
'\omega of Crank(r) & Coupler(b)'};
intitle=title0(driver+1);
val(abs(val)>10e+5)=NaN;
val(8:11,:)=abs(val(8:11,:));
figure(2); %第二繪圖區
clf;
subplot(2,2,1);
plot(th2,val(4,:),'k-');%crank angle or r1曲桿角
hold on;fact=round(max(val(5,:))/max(val(4,:))*10)/10;
plot(th2,val(5,:)/fact,'r-');% crank or coupler angle
xlabel(intitle);ylabel(title1(driver+1));
grid on
%
subplot(2,2,2);
plot(th2,val(6,:),'r-');%Omega of crank 曲桿角速度
fact=round(max(val(7,:))/max(val(6,:))*10)/10;
hold on;plot(th2,val(7,:)/fact,'b-');%Omega of coupler
xlabel(intitle);ylabel(title3(driver+1));
grid on;
%
subplot(2,2,3);
plot(th2,val(8,:),'k-');% vel of slider 滑塊速度
hold on;plot(th2,val(9,:),'r-');% vel of A
xlabel(intitle);ylabel(title2(1));
grid on;
%
subplot(2,2,4);
plot(th2,val(10,:),'k-');%Acc of slider 滑塊加速度
hold on;plot(th2,val(11,:),'r-');% Acc of A
xlabel(intitle);ylabel(title2(2));
grid on;
第九次作業結束
2 則留言:
你對程式的分析相當透徹,程式只是在控制小數位數,在應用上刪去應無大問題。另外界限條件可能有漏,你的補正正好可以改正過來。
做得很好。
感謝老師的指教
張貼留言